Our research interest
General Formalisms of Jahn-Teller and Pseudo-Jahn-Teller Vibronic Operators: Jahn-Teller and pseudo-Jahn-Teller interactions lead to far-reaching consequences in chemistry and physics. A graphical symbol of vibronic coupling is the conical intersection topology of potential energy surfaces as shown here.
More and more recent studies demonstrated the need of high order expansions of their Hamiltonian operators to describe the interactions satisfactorily. We endeavour to derive the arbitrarily high order expansion formulas of the Hamiltonian operators.
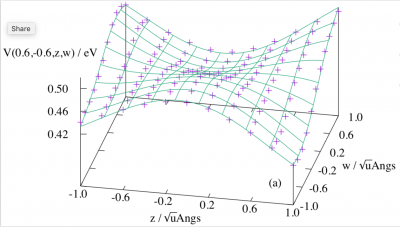
Shown in this figure are the calculated matrix elements (the markers) between an A1 and a T1 state in Td symmetry along an a2 and a t1 coordinate for a neopentane model, and the 10th order fitted surface using our derived formulas. For our latest advance in this frontier of research, please see J. Chem. Theory Comput. 2023, 19, 7776–7786; J. Chem. Phys. 2022, 156, 064104; J. Chem. Phys. 2021, 155, 224108; J. Chem. Theory Comput. 2021, 17, 4392-4402. Unified formalisms for all vibronic coupling and spin-orbit vibronic coupling problems in axial symmetries have been developed. A Python code, VHEGEN, which generates term-by-term expansions of the Hamiltonians, has also been developed. VHEGEN stands for Vibronic Hamiltonian Expansion GENerator.
Singlet Fission: Singlet fission is a phenomenon in organic photovoltaics that splits one singlet exciton to two triplet excitons. With this potential exciton number doubling, the photoelectric conversion efficiency is enhanced. We use quantum chemistry and quantum dynamics methods to probe the mechanism of singlet fission and to design chromophores for singlet fission.
Shown above are our recently designed intramolecular singlet fission chromophore and its simulated fission dynamics. It is the smallest model with only 18 non-H atoms. It undergoes the fastest singlet fission with a time scale of 16 fs. For our latest advance in this frontier of research, please see J. Phys. Chem. lett. 2024, 15, 43-50; J. Chem. Theory Comput. 2023, 19, 2092–2101; J. Phys. Chem. Lett. 2022, 13, 11076–11085.
Microscopic Superfluidity: We perform quantum Monte Carlo simulation of molecular rotor embedded in nanoscale clusters of 4He and para-H2, and gain understanding of the superfluid response of the surrounding bosons (4He and para-H2) to the rotation of the molecule. We are especially interested in the emerging superfluid response as the symmetry of the rotor is lower.
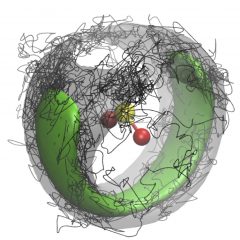
In this Figure, a SO2 molecule is surrounded by four para-H2 molecules. The pH2 density is represented by the green isosurface and one Feynman path configuration of the pH2 is represented by the black path. The pH2 exchange forms one path that contains all four pH2 molecules and the path winds around the SO2 molecule, resulting in superfluid response to the SO2 rotation. For more details about our work on microscopic superfluidity, please see J. Phys. Chem. Lett. 2013, 4, 18; J. Phys. Chem. Lett. 2013, 4, 2391; Rep. Prog. Phys. 2014, 77, 046601.
Spin-Orbit Coupling in Chemistry: We use natural spinors to explore the effects of spin-orbit coupling in chemistry. Natural spinors are the natural orbitals of spin-orbit coupled electronic wave functions. They can provide orbital explanations for spin-orbit coupling effects without running two-component relativistic quantum chemistry calculations.
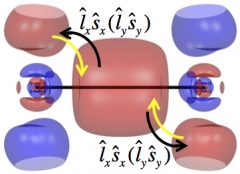
Shown in this figure are the σg (bonding) and πg (antibonding) orbitals of Tl2. Without spin-orbit coupling, the electronic configuration of Tl2 is σg2, with two electrons occupying the bonding orbital. The spin-orbit coupling transfers part of the two electrons to the πg orbital (through rotation, represented by the black curvy arrows) and reduces the bond strength.
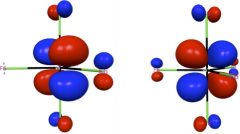
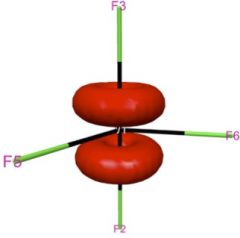Shown in the left two panels of this figure are the two degenerate e” orbitals of WF5, whose ground state electronic configuration is e”1. This partial occupation of degenerate orbitals is supposed to lead to the Jahn-Teller distortion, since each of the orbitals is not totally symmetric. However, spin-orbit coupling mixes these two orbitals and gives a totally symmetric distribution of electron density that maintains the D3h structure of WF5. For introduction and applications of natural spinors, please see J. Chem. Phys. 2011, 134, 214107; J. Chem. Theory Comput. 2011, 7, 2864; J. Chem. Theory Comput. 2012, 8, 3061.
Model Core Potential Development: Chemistry is mostly related to valence electronic structure of elements. This is summarized by Mendeleev’s periodic table: congeners that share the same valence electronic structure have similar chemical properties. Correspondingly, in quantum chemistry, we can simplify calculations by only treating valence electrons of atoms explicitly. The effects of the core electrons are hidden in the core pseudo potential.
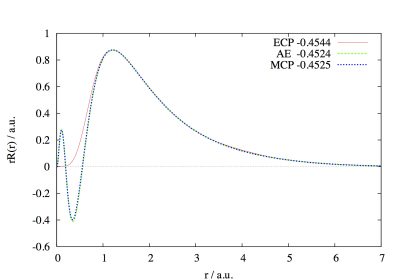Shown in this figure are the radial distribution functions of the Au 5d orbital calculated using the Effective Core Potential (ECP), Model Core Potential (MCP), and All Electron (AE, the reference) methods. The correspondingly calculated orbital energies are shown in the unit eV and they are all close. In ECP, since the Pauli exclusion between the core and valence electrons is not explicitly treated, the 5d orbital has no nodal structure in the small radius region. MCP retains the nodal structure through including the core-valence Pauli exclusion in its Hamiltonian. With the proper nodal structure, the properties that are sensitive to the valence electronic structure at the nuclear vicinity can be accurately evaluated using their genuine operators. These properties include spin-orbit coupling (SOC), nuclear magnetic resonance chemical shift, etc. We have endeavoured to develop SOC-adapted MCPs, with the objective to facilitate relativistic quantum chemistry calculations. Our developed MCPs cover all p-block elements up to the 6p elements. For more details about our work in MCP, please see J. Chem. Phys. 2009, 130, 204107; J. Chem. Phys. 2009, 131, 124109; J. Chem. Phys. 2010, 132, 074102; J. Chem. Phys. 2010, 133, 114107.
